0626_데이터분석 시험

카테고리 없음

by teminam 2023. 6. 21. 10:14

6. 데이터의 특징요약

- 'kid_score': 아이의 점수(kid_score)의 평균은 약 86.8이며, 최소값은 20,

최대값은 144입니다. 표준편차는 약 20.4입니다. 25% 분위수는 74, 50% 분위수는

90, 75% 분위수는 102입니다.

- 'mom_hs': 어머니의 학력(mom_hs)은 0 또는 1로 표현되며, 1의 비율(평균)은

약 78.6%입니다. 이는 학력을 가진 어머니의 비율을 나타냅니다.

- 'mom_iq': 어머니의 지능지수(mom_iq)의 평균은 약 100.0이며, 최소값은 71.

04, 최대값은 138.89입니다. 표준편차는 약 15.0입니다. 25% 분위수는 88.66,

50% 분위수는 97.92, 75% 분위수는 110.27입니다.

- 'mom_work': 어머니의 직장 근무 여부(mom_work)는 1, 2, 3, 4로 표현되며,

평균은 약 2.90입니다. 25% 분위수는 2, 50% 분위수는 3, 75% 분위수는 4입니다.

- 'mom_age': 어머니의 나이(mom_age)의 평균은 약 22.8이며, 최소값은 17,

최대값은 29입니다. 표준편차는 약 2.7입니다. 25% 분위수는 21, 50% 분위수는

23, 75% 분위수는 25입니다.

위 요약을 통해 아이의 점수, 어머니의 학력, 지능지수, 직장 근무 여부, 나이에

대한 통계적 특징을 파악할 수 있습니다.

# 8. 모든 변수에 대해 hist 그래프를 만들고 각 그래프에 따라 insight를 간단히 적어보세요
# 2점
# 평균이 좌우로 쏠린정도 등

# kid_score 히스토그램
plt.figure(figsize=(8, 6))
plt.hist(kidiq_df['kid_score'], bins=10, edgecolor='black')
plt.xlabel('Kid Score')
plt.ylabel('Frequency')
plt.title('Distribution of Kid Scores')
plt.show()
print("인사이트: 히스토그램은 아이들의 점수 분포를 보여줍니다. 
대부분의 점수는 상당히 높은 부분을 중심으로 분포하고 있으며, 90-100 사이에서 피크를 형성하고 있습니다.")

# mom_hs 히스토그램
plt.figure(figsize=(8, 6))
plt.hist(kidiq_df['mom_hs'], bins=2, edgecolor='black', align='mid', rwidth=0.8)
plt.xlabel('Mom HS')
plt.ylabel('Frequency')
plt.title('Distribution of Mom High School Education')
plt.xticks([0.25, 0.75], ['No HS', 'HS'])
plt.show()
print("인사이트: 이 히스토그램은 엄마의 고등학교 교육 수준의 분포를 나타냅니다. 데이터셋의 대부분의 엄마들은 고등학교를 졸업한 것으로 나타나며, 
'HS' 카테고리에서 높은 빈도를 보입니다.")

# mom_iq 히스토그램
plt.figure(figsize=(8, 6))
plt.hist(kidiq_df['mom_iq'], bins=10, edgecolor='black')
plt.xlabel('Mom IQ')
plt.ylabel('Frequency')
plt.title('Distribution of Mom IQ')
plt.show()
print("인사이트: 이 히스토그램은 엄마의 지능지수(IQ) 점수의 분포를 보여줍니다. 분포는 평균 IQ 점수 100을 중심으로 약간의 왼쪽으로 쏠리는 현상을 보이고 있으며,
80-90 범위에서 가장 높은 빈도를 보입니다.")

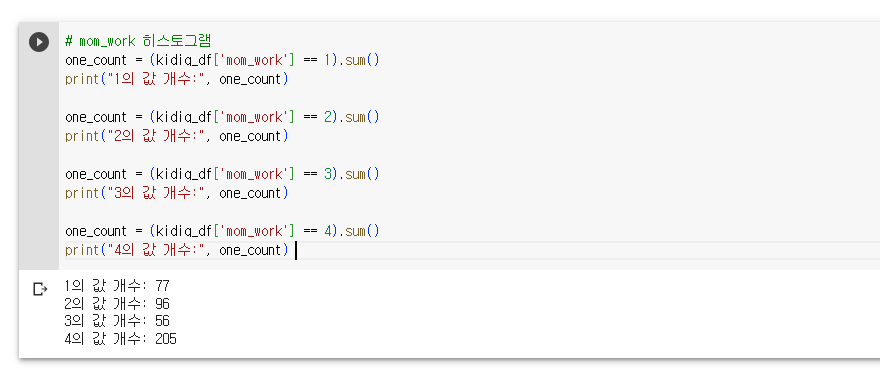
# mom_work 히스토그램
work_counts = kidiq_df['mom_work'].value_counts().sort_index()
x_labels = ['1Hour', '2Hour', '3Hour', '4Hour']

plt.figure(figsize=(8, 6))
plt.bar(x_labels, work_counts)
plt.xlabel('Mom Work')
plt.ylabel('Frequency')
plt.title('Distribution of Mom Work Status')
plt.show()

print("인사이트: 이 히스토그램은 엄마의 업무시간의 분포를 나타냅니다. 
대부분의 엄마들은 '4Hour' 범주에 속하는 것을 확인할 수 있습니다.")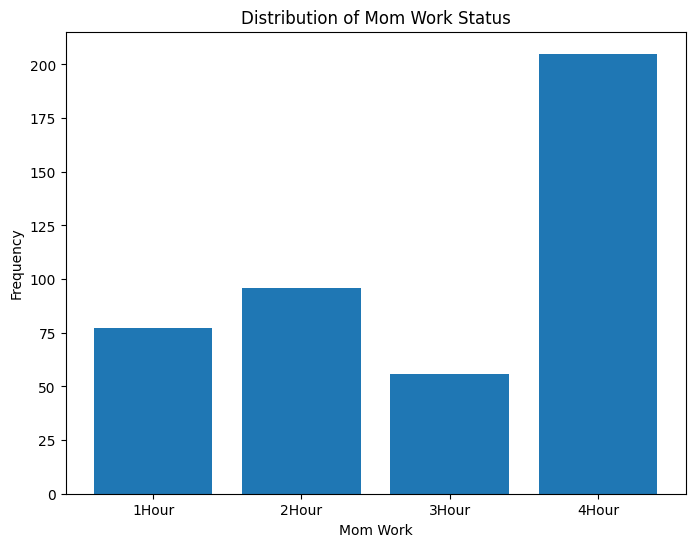

# mom_age 히스토그램
plt.figure(figsize=(8, 6))
plt.hist(kidiq_df['mom_age'], bins=10, edgecolor='black')
plt.xlabel('Mom Age')
plt.ylabel('Frequency')
plt.title('Distribution of Mom Age')
plt.show()
print("인사이트: 이 히스토그램은 엄마들의 나이 분포를 보여줍니다. 
데이터셋에서 대부분의 엄마들은 20대 초반에 속하는 것으로 보이며, 
22-23세 주변에서 빈도가 가장 높습니다.")

LinearRegression이란?

Linear Regression은 회귀 분석의 한 종류로, 종속변수와 한 개 이상의 독립변수

간의 선형 관계를 모델링하는 데 사용됩니다. 이 알고리즘은 주어진 독립변수와

종속변수 사이의 선형 관계를 가장 잘 표현하는 최적의 가중치와 절편을 찾는

과정을 거칩니다.

Linear Regression은 변수 간의 선형 관계를 가정하므로, 데이터가 선형성을

가지는 경우에 잘 작동합니다. 또한, 모델의 해석이 상대적으로 쉽고, 예측

결과를 설명하기 쉽다는 장점이 있습니다. 그러나 비선형 관계를 가지는

데이터에는 적합하지 않을 수 있습니다.

이러한 Linear Regression 모델은 다양한 응용 분야에서 사용되며, 예측, 추정,

변수 간 상관 관계 분석 등에 활용됩니다.

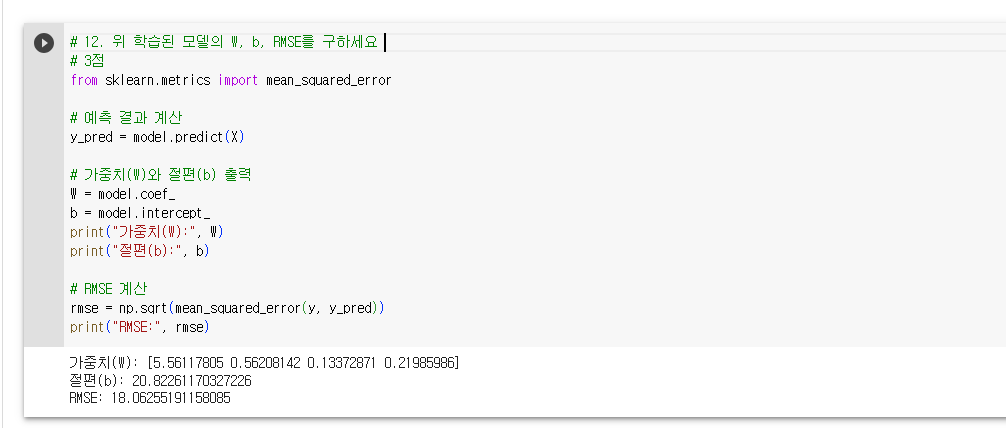
# 14. 위 결과의 w, b를 이용해 K-Fold(k=5)를 이용하여 RMSE의 평균 값을 확인하세요
# 3점

from sklearn.model_selection import KFold

# 독립변수 X와 종속변수 y 설정
X = kidiq_df[['mom_hs', 'mom_iq', 'mom_work', 'mom_age']]
y = kidiq_df['kid_score']

# K-Fold 교차 검증 설정
k = 5
kf = KFold(n_splits=k)

# RMSE를 저장할 리스트 생성
rmse_scores = []

# K-Fold 교차 검증을 통한 예측 및 평가
for train_index, test_index in kf.split(X):
    # 훈련 데이터와 테스트 데이터 분할
    X_train, X_test = X.iloc[train_index], X.iloc[test_index]
    y_train, y_test = y.iloc[train_index], y.iloc[test_index]

    # LinearRegression 모델 생성 및 학습
    model = LinearRegression()
    model.fit(X_train, y_train)

    # 테스트 데이터에 대한 예측
    y_pred = model.predict(X_test)

    # RMSE 계산 및 저장
    rmse = np.sqrt(mean_squared_error(y_test, y_pred))
    rmse_scores.append(rmse)

# RMSE 평균 계산
rmse_mean = np.mean(rmse_scores)

print("RMSE Mean:", rmse_mean)

# 15. 독립변수에 가중치(mom_hs * mom_iq_c) 변수를 추가하고 14번에 대해 다시 확인하세요
# 3점
# 가중치 이름은 맘대로 적고, 엄마의 아이큐 차이와 hs값 곱을 새롭게 변수로 만들고 14번의 평균 값 구해보기.

# 독립변수 X와 종속변수 y 설정
X = kidiq_df[['mom_hs', 'mom_iq', 'mom_work', 'mom_age', 'mom_iq_c']]
X['mom_hs_mom_iq_c'] = X['mom_hs'] * X['mom_iq_c']
y = kidiq_df['kid_score']

# K-Fold 교차 검증 설정
k = 5
kf = KFold(n_splits=k)

# RMSE를 저장할 리스트 생성
rmse_scores = []

# K-Fold 교차 검증을 통한 예측 및 평가
for train_index, test_index in kf.split(X):
    # 훈련 데이터와 테스트 데이터 분할
    X_train, X_test = X.iloc[train_index], X.iloc[test_index]
    y_train, y_test = y.iloc[train_index], y.iloc[test_index]

    # LinearRegression 모델 생성 및 학습
    model = LinearRegression()
    model.fit(X_train, y_train)

    # 테스트 데이터에 대한 예측
    y_pred = model.predict(X_test)

    # RMSE 계산 및 저장
    rmse = np.sqrt(mean_squared_error(y_test, y_pred))
    rmse_scores.append(rmse)

# RMSE 평균 계산
rmse_mean = np.mean(rmse_scores)

print("RMSE Mean:", rmse_mean)

16. 14번, 15번에 대해 결과를 비교하고 다른 결과에 대해 설명하세요

* RMSE Mean: 18.839711075764928

* RMSE Mean: 18.607540796337446

처음에 가중치(mom_hs * mom_iq_c) 변수를 추가하지 않았을 때의 RMSE 평균 값은

18.839711075764928이고, 가중치 변수를 추가한 후의 RMSE 평균 값은 18.

607540796337446입니다. 이 두 값이 서로 다른 이유와 이러한 작업의 필요성에

대해 설명해드리겠습니다.

1. 서로 다른 값이 유도되는 이유:

- 가중치(mom_hs * mom_iq_c) 변수를 추가한 후의 RMSE 평균 값이 더 낮게

나타난 것은, 가중치 변수의 추가로 인해 모델의 설명력이 개선되었기

때문입니다.

- 'mom_hs' 변수는 엄마의 고등학교 교육 여부를 나타내며, 'mom_iq_c' 변수는

엄마의 IQ 점수와 평균 IQ 점수의 차이를 나타냅니다.

- 이 두 변수의 곱은 엄마의 고등학교 교육 여부와 IQ 점수 차이를 함께

고려한 새로운 변수로 볼 수 있습니다.

- 가중치 변수를 추가함으로써 모델은 엄마의 교육 수준과 IQ 점수 차이를

고려하여 더 정확한 예측을 수행할 수 있게 되었습니다.

2. 작업의 필요성:

- 독립변수에 가중치 변수를 추가하는 작업은 다양한 이유로 필요할 수

있습니다.

- 가중치 변수를 추가함으로써 독립변수들 간의 상호작용을 고려할 수

있습니다. 이는 실제 데이터에서 복잡한 관계를 반영하고 모델의 설명력을

향상시킬 수 있습니다.

- 또한, 가중치 변수를 통해 도메인 지식이나 경험적인 가정을 모델에 반영할

수 있습니다. 가중치 변수는 도메인 전문가의 지식을 활용하여 모델을

조정하거나 특정 변수들의 중요성을 강조할 수 있습니다.

- 가중치 변수의 추가는 모델의 유연성을 높이고, 보다 정확한 예측을

가능하게 합니다.

결론적으로, 독립변수에 가중치 변수를 추가하면 모델의 설명력과 예측 성능을

향상시킬 수 있습니다. 이를 통해 데이터의 복잡한 상호작용을 고려하고 도메인

지식을 모델에 반영할 수 있습니다. 따라서, 적절한 가중치 변수의 선택과

추가는 모델의 성능 향상을 위해 중요한 작업입니다.

18. 결과해석

테스트 데이터에 모델을 적용한 결과, 예측된 아이의 IQ 값은 다음과 같습니다:

1. 첫 번째 테스트 데이터: 예측된 아이의 IQ 값은 약 94입니다.

2. 두 번째 테스트 데이터: 예측된 아이의 IQ 값은 약 80입니다.

3. 세 번째 테스트 데이터: 예측된 아이의 IQ 값은 약 79입니다.

4. 네 번째 테스트 데이터: 예측된 아이의 IQ 값은 약 92입니다.

모델은 주어진 독립 변수에 기반하여 아이의 IQ를 예측한 것입니다. 예측된 값은

부모의 IQ, 학력, 직장 근무 상태, 부모의 나이 등을 고려한 결과입니다. 이

예측 결과는 해당 테스트 데이터에 대한 모델의 예측 성능을 나타냅니다.

이러한 예측 결과는 주어진 독립 변수와 모델의 학습을 통해 유추된 것입니다.

테스트 데이터에서는 부모의 IQ와 관련된 변수인 'mom_iq'와 'mom_iq_c'를

사용하여 아이의 IQ를 예측하였습니다. 이를 통해 부모의 IQ가 높을수록 예측된

아이의 IQ도 높아지는 경향을 보였습니다.

결과적으로, 부모의 IQ와 아이의 IQ는 어느 정도 연관이 있음을 알 수 있습니다.

모델이 테스트 데이터를 기반으로 예측한 결과는 일정한 경향성을 보여주고

있으며, 부모의 IQ가 아이의 IQ에 영향을 줄 수 있다는 것을 시사합니다.

# 18. 위 결과에 대해 설명하고, 결론(부모의 IQ와 아이의 IQ는 연관이 있을까?)에 대해 결과를 시각적으로 표현하세요
# 10점
import seaborn as sns
import matplotlib.pyplot as plt

# 산점도 그래프
plt.figure(figsize=(8, 6))
sns.scatterplot(data=kidiq_df, x='mom_iq', y='kid_score')
plt.xlabel("Parents IQ")
plt.ylabel("Kids IQ")
plt.title("Relationship between Parent's IQ and Child's IQ")
plt.show()

# 히트맵
plt.figure(figsize=(8, 6))
corr_matrix = kidiq_df[['mom_iq', 'kid_score']].corr()
sns.heatmap(corr_matrix, annot=True, cmap='coolwarm')
plt.title("Correlation Heatmap: Parent's IQ vs. Child's IQ")
plt.show()

19. Cross validation은 어떨 때 유의미하게 사용할 수 있는지 설명하세요

앞서 나온 결과를 통해 Cross validation이 어떤 상황에서 유의미하게 사용될 수

있는지 설명해보겠습니다.

우선, Cross validation은 모델의 일반화 성능을 평가하기 위해 유의미하게

사용될 수 있습니다. 일반적으로 단일 분할로만 데이터를 사용하여 모델을

평가하면 해당 데이터에 대해서만 잘 동작하는 모델을 얻을 수 있습니다. 그러나

이는 모델의 실제 성능을 정확하게 파악하기 어렵게 만들 수 있습니다.

Cross validation은 데이터를 여러 개의 겹치지 않는 부분 집합으로 나누어

모델을 여러 번 학습하고 평가하는 방법입니다. 이를 통해 데이터를 더 잘

활용하며, 모델의 성능을 더 신뢰할 수 있는 방식으로 평가할 수 있습니다. 앞서

구현한 K-Fold cross validation을 통해 모델의 성능을 평가한 결과 RMSE의 평균

값을 얻었습니다. 이 값은 모델의 일반화 성능을 나타내며, 다른 데이터에

대해서도 비슷한 성능을 기대할 수 있음을 나타냅니다.

또한, Cross validation은 하이퍼파라미터 튜닝에도 유의미하게 사용될 수

있습니다. 모델에는 여러 가지 하이퍼파라미터가 있으며, 이들을 적절히

설정하는 것은 모델의 성능에 큰 영향을 미칩니다. 앞서 구현한

RandomizedSearchCV를 통해 최적의 하이퍼파라미터를 찾았고, 이를 바탕으로

모델을 학습시켰습니다. Cross validation은 다양한 하이퍼파라미터 조합에 대해

모델을 평가하고, 최적의 조합을 선택하는 데에 활용됩니다.

마지막으로, Cross validation은 데이터의 한정적인 경우에도 유의미하게 사용될

수 있습니다. 데이터가 제한적인 경우에는 모델을 단일 분할로만 평가하면

과적합의 문제가 발생할 수 있습니다. Cross validation은 데이터를 여러 부분

집합으로 나누어 모델을 평가하므로, 주어진 한정된 데이터를 더 효과적으로

활용하여 모델의 일반화 성능을 신뢰할 수 있게 합니다.

따라서, 이러한 결과들을 토대로 Cross validation은 모델의 일반화 성능 평가,

하이퍼파라미터 튜닝, 한정적인 데이터셋에서의 모델 평가 등 다양한 상황에서

유의미하게 사용될 수 있음을 알 수 있습니다.

20. Cross validation 결과에서 특정 Fold에만 결과가 잘 나오는 경우 어떻게 처리해야 하는지 설명하세요(10점)

Cross validation 결과에서 특정 Fold에만 결과가 잘 나오는 경우, 다음과 같은

접근 방법을 고려해볼 수 있습니다:

1. 추가 데이터 수집: 해당 Fold에서의 결과가 좋지 않은 이유는 해당 데이터에

특정한 패턴 또는 편향성이 존재할 수 있기 때문일 수 있습니다. 이 경우, 해당

Fold에서의 결과를 개선하기 위해 추가 데이터를 수집하고, 불균형한 데이터

분포를 보완할 수 있습니다.

2. 데이터 전처리: 특정 Fold에서의 결과가 좋지 않은 경우, 해당 Fold에서의

데이터에 대해 전처리 작업을 진행하여 모델이 더 좋은 결과를 도출할 수 있도록

도움을 줄 수 있습니다. 이는 이상치 제거, 이중화 처리, 정규화 등 다양한

방법을 포함할 수 있습니다.

3. 모델 수정 또는 교체: 특정 Fold에서의 결과가 계속해서 좋지 않은 경우,

해당 Fold에서 잘 동작하지 않는 모델의 문제일 수 있습니다. 모델 구조,

하이퍼파라미터 등을 수정하거나 다른 모델을 시도해보는 것이 좋습니다. 예를

들어, 복잡한 모델을 사용하거나 모델의 용량을 조절하여 과적합을 완화시킬 수

있습니다.

4. 앙상블 기법 사용: 특정 Fold에서의 결과가 좋지 않을 수 있는데, 이는 해당

Fold에서의 데이터에 대해 모델이 취약하거나 특정한 상황에 대응할 수 없는

경우일 수 있습니다. 이런 경우 앙상블 기법을 사용하여 다양한 모델의 예측

결과를 결합하여 더 강력한 예측을 할 수 있습니다. 예를 들어, 다양한 모델의

예측값을 평균 또는 가중 평균하여 최종 예측 결과를 얻을 수 있습니다.

5. 문제 재정의: 특정 Fold에서의 결과가 계속해서 좋지 않다면, 모델이 풀고자

하는 문제의 정의 또는 목표를 재검토할 필요가 있을 수 있습니다. 문제의

복잡성, 변수의 선택, 목표 설정 등을 재평가하여 더 적합한 방향으로 모델을

조정할 수 있습니다.

위의 접근 방법은 특정 Fold에서의 결과가 좋지 않은 경우에 대처할 수 있는 몇

가지 일반적인 방법입니다. 그러나 상황에 따라 적절한 조치가 달라질 수

있으므로, 실제 문제와 데이터에 따라 조정하고 실험하는 것이 중요합니다.

테미남

고정 헤더 영역

메뉴 레이어

메뉴 리스트

검색 레이어

검색 영역

상세 컨텐츠

본문 제목

본문

추가 정보

인기글

최신글

티스토리툴바